Введение
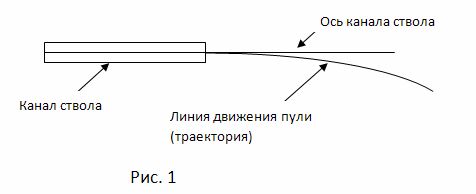
Пуля, получив при вылете из канала ствола определенную начальную скорость, движется по инерции в заданном направлении. Если бы полет пули совершался в безвоздушном пространстве, и на нее не действовала сила тяжести, пуля двигалась бы прямолинейно, равномерно и бесконечно. Однако, на пулю, летящую в воздухе, действуют силы, которые изменяют скорость ее полета и направление движения. Этими силами являются сила тяжести и сила сопротивления воздуха. Вследствие совместного действия этих сил пуля перемещается в воздухе по кривой линии, проходящей ниже направления оси канала ствола (рис. 1).
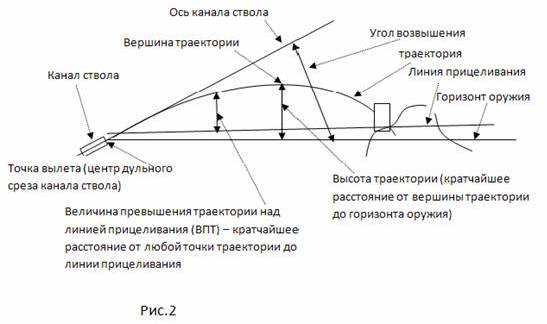
Становится очевидно, что для того, чтобы пуля пролетела определенное расстояние и поразила цель, необходимо направить ствол оружия выше цели. Для этого нужно, чтобы ось канала ствола и плоскость горизонта оружия составляли некоторый угол, который называется углом возвышения (рис. 2).
В ходе настоящей работы предполагается рассмотреть два вопроса.
При поступлении пистолета в какую либо воинскую часть, ОВД, и т. д., пистолет приводят к нормальному бою, т. е. посредством манипуляций с целиком (положение и форма мушки не меняются) производят "настройку пистолета" таким образом, чтобы средняя точка попадания была выше точки прицеливания на 12,5 см (при стрельбе с 25 м) (рис. 3).
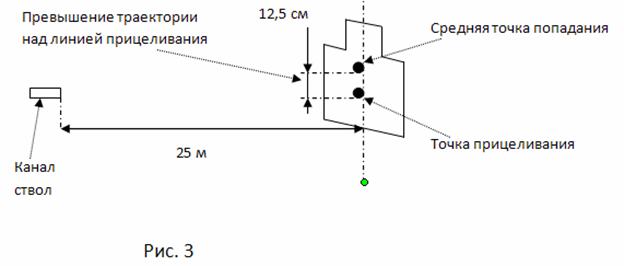
Причем приведение пистолета к нормальному бою производится таким образом, что с увеличением расстояния до мишени расстояние между точкой прицеливания и средней точкой попадания увеличивается (до тех пор, пока ВПТ не будет равна максимальной высоте траектории, затем, с увеличением расстояния до мишени ВПТ будет уменьшаться). И, наоборот, с уменьшением расстояния до мишени, расстояние между точкой прицеливания и средней точкой попадания уменьшается.
Известно, что у ПМ, приведенного к нормальному бою, соответствие ВПТ и расстояния до мишени следующее:
| Расстояние; м |
ВПТ; см |
| 10 |
5.0 |
| 15 |
7.8 |
| 20 |
10.2 |
| 25 |
12.5 |
| 30 |
13.9 |
| 40 |
16.0 |
Нами предполагается провести стрельбы с трех рубежей - 10 м, 20 м, 30 м, и полученные результаты вычисления ВПТ сравнить с данными из таблицы.
Ход работы:
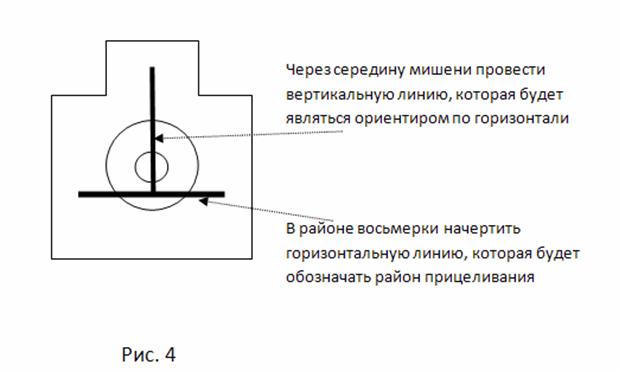
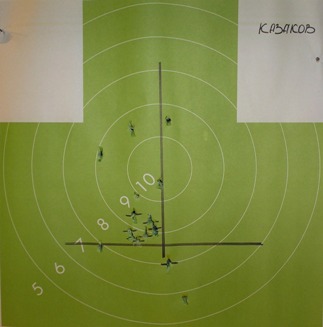
1. На всех трех рубежах используется грудная мишень № 4, предварительно особым образом подготовленная (рис. 4).
2. На каждом рубеже предполагается выполнить по 8 выстрелов.
После каждой серии стрельб предполагается отмечать пробоины, соответствующие своей серии (одной серии соответствует стрельба с одного рубежа). При необходимости можно использовать новую мишень, предварительно подготовленную (рис. 4). После каждой серии стрельб предполагается фотографирование мишеней.
Итак, нами были выполнены стрельбы с трех рубежей - 10 м, 20 м, 30 м.
* При стрельбе с 10 м было произведено 8 выстрелов, при подсчете ВПТ учитывались все пробоины. Вычисление ВПТ производилось следующим образом:
1) посредством метода вычисления нами была определена средняя точка попадания;
2) от средней точки попадания был опущен перпендикуляр к линии, обозначающей район прицеливания, величина перпендикуляра была взята как среднее значение ВПТ.
 При подсчете среднее значение ВПТ было определено равным 2,2 см. В свою очередь, табличное значение ВПТ для данного расстояния составляет 5 см. Т. е. разница между табличным значением и значением, полученным после проведения стрельбы, составила 2,8 см. Безусловно, в данных условиях разница достаточно велика, но она ожидаема и обуславливается определенными факторами, которые необходимо учитывать. К таким факторам можно отнести следующие:
1. К стрельбе был привлечен курсант, имеющий малый опыт выполнения стрельбы.
2. Пистолет не был специально подготовлен.
3. Количество выстрелов было не очень велико, т. е. в расчетах участвовало небольшое количество значений.
Но, так или иначе, вывод после стрельбы с 10 м можно сделать следующий: при стрельбе примерно до 10 м ВПТ достаточно заметна, но не очень велика и, в некоторых случаях может не учитываться.
 * При стрельбе с 20 м было произведено также 8 выстрелов и, при подсчете ВПТ учитывались также все пробоины. Вычисление ВПТ было аналогично вычислению ВПТ при стрельбе с 10 м. Среднее значение ВПТ при стрельбе с 20 м было определено равным 9,8 см. Табличное значение - 10,2 см. Следовательно, разница между табличным значением ВПТ и ВПТ рассчитанной после выполнения стрельбы составила 2,8 см. Логично, что данные из таблицы не совпали с данными, полученными после выполнения стрельбы, т. к. стрельбу выполняет человек, а человек является живым существом и на него действуют различные факторы, следовательно, невозможно в момент выстрела удерживать пистолет в руках совершенно неподвижно. При стрельбе пистолет колеблется, т. к. по мышцам рук постоянно проходят нервные импульсы, кровь движется по жилам и т. д., поэтому умение сосредотачиваться и ровно удерживать пистолет очень важно для выполнения качественной стрельбы. Данное умение приходит в ходе многочисленных тренировок, поэтому, учитывая, что в данных условиях курсант, выполняющий стрельбу, обладает малым опытом, мы можем считать отклонение в 1,2 см от табличного значения небольшим. Основной вывод: при стрельбе с данного рубежа ВПТ имеет достаточно большое значение и его, безусловно, необходимо учитывать.
 * При стрельбе с 30 м было произведено 8 выстрелов, при подсчете ВПТ учитывались все пробоины. Вычисление ВПТ аналогично вычислениям ВПТ после стрельбы с 10 м и 20 м. При подсчете среднее значение ВПТ при стрельбе с 30 м было определено равным 9 см, табличное значение - 13,9 см. Разница между табличным значением ВПТ и значением ВПТ, измеренным после стрельбы составила 4,9 см. Следует отметить, что у нас почти совпали величины ВПТ, измеренные после стрельбы с 20 м и с 30 м, причем значение ВПТ для расстояния 20 м у нас получилось немного больше, но опять же следует вновь вспомнить, что в данной ситуации человеческий фактор играет значительную роль. Человеческий фактор, в нашем понимании, включает в себя уровень подготовки стрелка, его эмоциональный настрой, умение стрелка контролировать себя, концентрировать внимание в момент выстрела. Наряду с человеческим (субъективным) фактором можно выделить объективный фактор, который включает в себя качество оружия, состояние оружия, качество боеприпасов, освещение и т. д.
Итак, мы в теории и на практике рассмотрели явление превышения траектории над линией прицеливания и пришли к выводу о том, что данное явление имеет большое значение при выполнении стрельбы. На практике мы подтвердили теоретические расчеты относительно того, что при стрельбе с небольших расстояний ВПТ не очень выражается, но при стрельбе с больших расстояний (например, свыше 10 м) ВПТ достаточно сильно проявляется и ее необходимо учитывать при стрельбе, т. к. в данных условиях от этого напрямую зависит результативность стрельбы.
Для того чтобы пуля летела в нужном направлении и поражала предполагаемый район мишени, на оружии существует прицельное приспособление, состоящее из мушки и целика. При стрельбе необходимо учитывать расстояние до мишени а, следовательно, ВПТ, также необходимо выставлять "ровную мушку" (рис. 5).
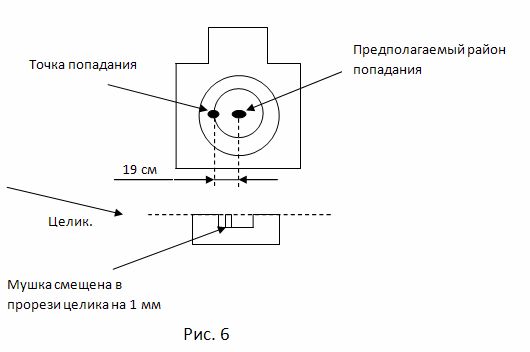
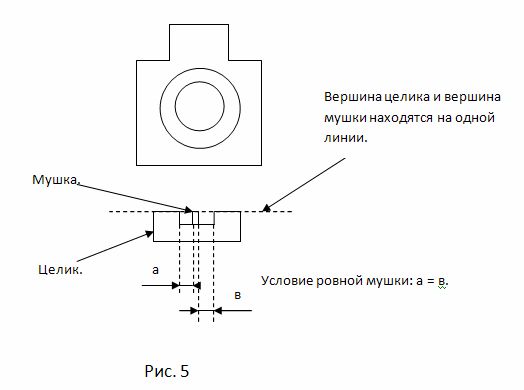 При условии, что выставлена "ровная мушка" и в момент выстрела она не смешается (остается ровной), пуля летит без отклонения по горизонтали (побочные явления, такие как деривация или боковой ветер не учитываем) и без отклонения по вертикали (учитывая ВПТ). Если величины а и в (рис. 5) не равны, то при выстреле пуля отклонится по горизонтали в ту или иную сторону (если, а < в, то влево; если, а > в, то вправо). И аналогично, если вершины мушки и целика не будут находиться на одной линии, то будет происходить смещение пули по вертикали от предполагаемой точки попадания. Поэтому при стрельбе необходимо выдерживать "ровную мушку" для выполнения более качественной и результативной стрельбы, т. к. известно, что при стрельбе с 25 м смещение мушки в прорези целика по горизонтали на 1 мм дает отклонение точки попадания от предполагаемого района попадания на 19 см (рис. 6).
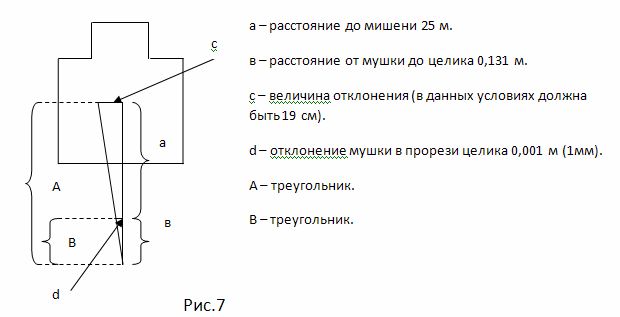
С точки зрения геометрии это явление можно объяснить следующим образом (рис. 7):
Треугольники А и В подобные. Нам известны величины а, в, d. Найдем величину с - величину отклонения. Исходя из вышеназванных условий мы можем составить пропорцию:
а/в = с/d,
следовательно с = (а*d)/в - соответственно с = (25*0,001)/0,131=0,19084 м или 19 см, таким образом мы теоретически обосновали зависимость отклонения пули от смещения мушки в прорези целика (зависимость отклонения пули от смещения мушки в прорези целика аналогична).
Из формулы видно, что величина отклонения пули прямо пропорциональна расстоянию до мишени (рис. 7 - величина а). Вышерассмотренное явление отклонения пули, на наш взгляд, и определяет величину рассеивания пуль по горизонтали и по вертикали. Таким образом, мы теоретически, применяя метод моделирования и математические законы, объяснили зависимость рассеивания пуль от расстояния до мишени.
Можно сделать следующий вывод, что при стрельбе (в момент выстрела) необходимо удерживать ровную мушку для того, чтобы стрельба была точной и кучной (т. е. величина рассеивания пуль минимальна). Но, безусловно, при стрельбе человеку удерживать идеально ровную мушку достаточно сложно, поэтому так или иначе, в момент выстрела происходит хотя бы незначительное смещение мушки, что и вызывает явление рассеивания пуль. Из теоретических расчетов, изложенных выше, мы видим, что с увеличением расстояния до мишени явление рассеивания пуль, при постоянной величине смещения мушки, будет становиться более выраженным.
Нам необходимо на практике проверить наши теоретические выводы. В качестве материала для работы мы взяли мишени, которые использовали при стрельбе в ходе рассмотрения вопроса № 1 (см. фото выше). Для каждой серии стрельб (с рубежей 10 м, 20 м, 30 м) мы посредством метода вычисления определили среднюю точку попадания. Затем, для каждой серии, мы от средней точки попадания измеряли кратчайшее расстояние до пробоин.
При стрельбе с 10 м результаты получились следующие: четыре пробоины находились от средней точки попадания на расстоянии, не превышающем 2 см; три пробоины на расстоянии, не превышающем 2,5 см. Одна пробоина находилась от средней точки попадания на расстоянии 6,7 см.
При стрельбе с 20 м результаты получились следующие: две пробоины находились от средней точки попадания на расстоянии, не превышающем 4 см (от 2,5 см до 4 см); одна пробоина на расстоянии, не превышающем 7 см; две пробоины на расстоянии, не превышающем 9 см; две пробоины на расстоянии, не превышающем 12 см. Одна пробоина находилась от средней точки попадания на расстоянии 19,9 см.
При стрельбе с 30 м результаты получились следующие: одна пробоина находились от средней точки попадания на расстоянии, не превышающем 4 см; четыре пробоины на расстоянии, не превышающем 9 см (от 7 см до 9 см); две пробоины на расстоянии, не превышающем 12 см. Одна пробоина находилась от средней точки попадания на расстоянии 15,1 см.
Таким образом, из результатов стрельб мы видим, что при стрельбе на малом расстоянии (10 м) величина рассеивания пуль не так велика, что подтверждает теоретические расчеты. При стрельбе с больших расстояний (20 м, 30 м) величина рассеивания пуль уже достаточно заметна, что также подтверждает теоретические расчеты.
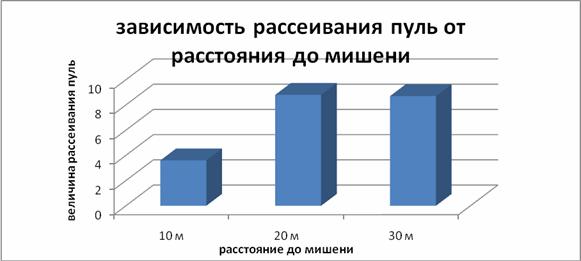
Для наглядности представим гистограмму, отражающую зависимость величины рассеивания пуль от расстояния до мишени. Для этого найдем среднее арифметическое значение всех кратчайших расстояний от средней точки попадания до пробоин (для каждой серии стрельб). Это среднее арифметическое значение будет являться средней величиной рассеивания пуль для каждой серии стрельб. Средние значения величины рассеивания пуль для различных рубежей получились следующими: 10 м - 3,6 см, 20 м - 8,8 см, 30 м - 8,7 см. на основании полученных данных построим гистограмму - рис. 8.
Заключение
Учитывая теорию и практику стрельбы, можно сказать следующее, что при стрельбе необходимо строго следовать выработанной методике выполнения стрельб, а для этого необходимо знать материальную часть оружия, основные положения внутренней и внешней баллистики, правила и приемы стрельбы. Все эти знания теории в системе с практикой сформируют умение у стрелка выполнения качественной стрельбы. Далее, в процессе постоянных тренировок и совершенствования собственной техники стрельбы, на основе знаний и умений сформируется навык выполнения качественной и результативной стрельбы.
|